Multiscale methods for long time wave propagation

Some background
Physical situations occurring in complicated media are usually modeled in a multiscale framework. Indeed, while the quantities of interest are often macroscopic, the microscopic structure of the medium influences the physical process and must be incorporated in the model. However, multiscale models come with the difficulty of their discretization: to be accurate, standard methods such as finite elements or finite differences require a grid resolving the whole medium at the microscopic scale, which lead to a prohibitive cost. Therefore, more sophisticated numerical methods are needed.
For wave phenomena, multiscale features are found in several important applications such as medical imaging, seismic inversion, or the manufacture of composites. In these situations the wavelengths of the propagating waves are much larger than the wavelengths of the medium in which they propagate. Several multiscale methods are available in the litterature, each of which come with pros and cons (see e.g. this review). In this research we focus on the finite element heterogeneous multiscale method (FE-HMM). The FE-HMM relies on homogenization, a mathematical theory ensuring the existence of effective propagating waves. Hence, the macroscopic behavior of the propagating waves can be described by waves that do not depend on the microscopic variation of the medium: the effective waves called homogenized waves. The FE-HMM is built to approximate the homogenized waves by approximating a homogenized medium locally in microscopic sampling domains. Thanks to this strategy, the computational cost of the method is independent of the microscopic scale. Furthermore, the approximation is proved to be accurate in media where the microscopic and macroscopic scales are clearly distinct.
My research
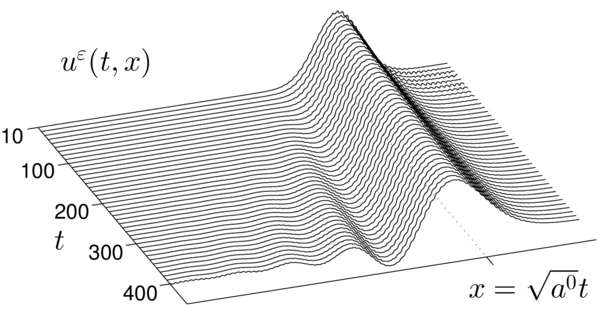
When we want to approximate the waves at long times, classical homogenization fails to capture additional dispersion that develop in the effective behavior of the waves. This is illustrated in the following pictures (for more details see Chapter 4 of my thesis).

In picture (a), we see the time evolution of the waves that we want to approximate using homogenization (displayed in a moving frame around a pulse). These waves propagates in a simple periodic medium that oscillates at the microscopic scale. We observe that indeed as time increases dispersion appear in the macroscopic behavior of the waves. In picture (b) is displayed the time evolution of the corresponding homogenized solution. While the wavespeed of the main pulse is accurate, the dispersion is not captured.
As classical homogenization does not describe accurately the long time dispersion, the FE-HMM, which approximate the homogenized wave, can not be expected to provide a good approximation for large times. The global objective of this research is to develop a enhanced version of the method that describes the dispersion.
The key towards this objective is to understand deeply this dispersion effect by deriving an effective model to improve the homogenized one. In fact, the classic homogenization can be understood as a zero-th order effective model and we are looking for the higher order ones. An important result that we derived proves that for any time (arbitrarily long) there exists a family of effective models that describes well the dispersion in periodic media (joint work with Prof. A. Abdulle, see this paper and this one for the maths). We also provided efficient algorithms to compute the effective waves in these media. Coming back to the example above, with this result we now obtain the following pictures:

Picture (a) is the same as before. Picture (b) is displayed the time evolution of a first order effective model (one in the family). Observe that this time the macroscopic dispersion in the fine scale wave (black curves in the left picture) is accurately captured.
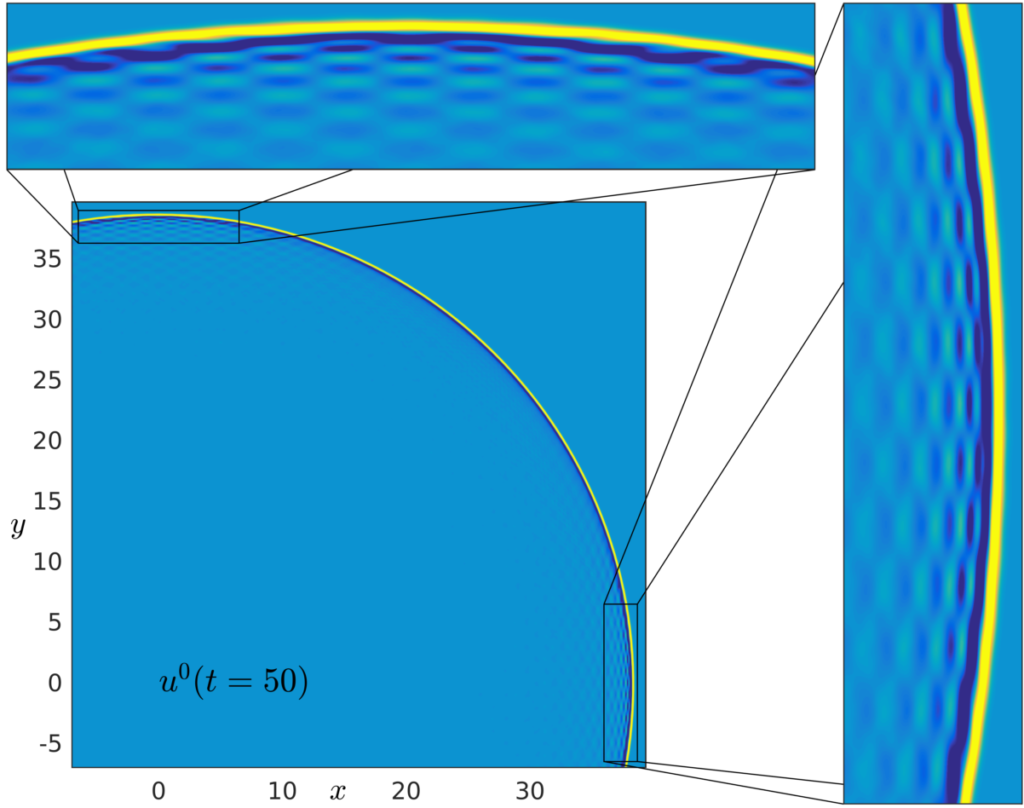
These results were obtained for periodic media. We extended them to locally periodic media, which allow for a macroscopic deformation of the microscopic structure (the maths in this paper). Here are pictures to illustrate the benefit of this result.
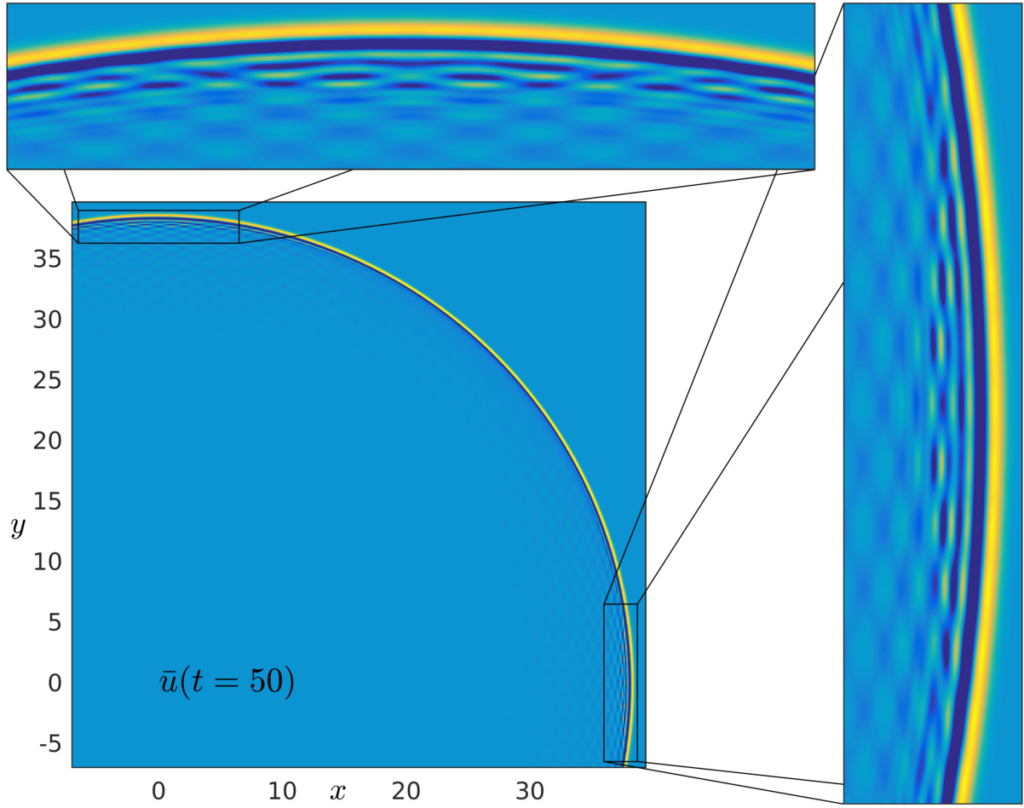
We consider an initial pulse centered at the origin \((0,0)\), and let it evolve in a locally periodic medium.
In picture (a) is displayed a snapshot of the homogenized waves \(u^0\) at time \(t=50\). Observe that the pulse has propagated in all directions: the front waves appear in yellow on the picture. The bumps that we can see behind the front waves correspond to the macroscopic variation of the medium. In picture (b) is the corresponding effective waves of order 1: \(\bar{u}\). The global behavior is similar, but it captures additional macroscopic dispersive effects, visible in the zooms.